"How to make out the SAR interferogram?"
Principle of InSAR / Intermediate Course1
The results by InSAR analysis is mostly shown as a picture with colored fringes like Figure 7. It is similar to rainbow-colored fringes formed on a soap bubble or a film of oil floating on the water.
There is deformation in the area where the color turns from blue to red to yellow to green (the display sequence depends on a computer software in use). At this time, please pay attention to the fact that rainbow-colors of fringes repeat cyclically, turning from blue to red to yellow to green and turning back to blue.
Method of visualization
InSAR does not allow us to know an absolute distance. Only The phase of a radar wave is measured. Because the phase describes its position within one wave cycle, we cannot know the number of waves which the phase is contained. The phase is recorded in values between 0 and 360 degrees to describe its position within one wave cycle.
The color of fringes in an interferogram show the difference in phase resulted from the difference in distance between two SAR data at the point. For example, an area where the difference in phase is 0 degree is showed in light-blue color, 60 degrees showed in blue color, 180 degrees showed in red color, and so on. If the difference in phase is 360 degrees, the distance that a radio wave travels back and forth between a radar and the ground changes by just one wavelength.
Because the radar installed on the Japanese SAR satellite ALOS ("Daich") has a wavelength of 23.6cm, the phase difference of 360 degrees is equivalent to the movement of 11.8cm (one-way distance is a half of round-trip one). Likewise, the point whose difference in phase is 60 degrees moves 2.0cm (23.6*(60/360)/2≒2.0).
The difference in phase is equivalent to the amount of deformation in this way, the color of fringes represents the magnitude of deformation at the point.
The phase returns to 0 degree when it increases up to 360 degrees. That means the deformation which is equal to the integral multiple of 360 degrees just has the same phase. This is because radar waves which have the same waveform are indistinguishable from each other.
The difference of phase varies with the periodicity of 360 degrees, so the surface deformation resulted from InSAR has arbitrary constants of the integral multiple of the one-half wavelength.
For example, if the color of a point in an interferogram of ALOS is equivalent to the movement of 5.0 cm, the movement of the point is actually 5.0±11.8*n cm (n is an integer).
This arbitrary property is resolved as follows.
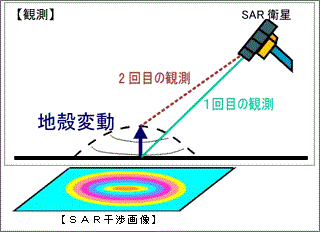
Figure 7. Crustal deformation and SAR interferogram
* It is the phase that InSAR measures!
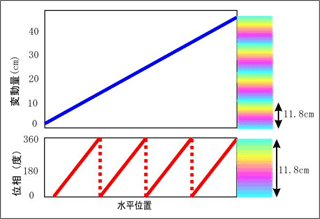
Figure 8. Phase change measured by L-band
(wavelength of 23.6cm) InSAR
* Actual movement is wrapped into the phase cycle (11.8cm)
We conclude that based on the color of the point where there is no surface deformation in a SAR interferogram, the point where returns first to the base color has the phase difference of 360 degree, the movement of 11.8 cm. Two cycle of color indicates 23.6 cm, twice 11.8 cm. Repeating this procedure, we can find the real absolute amount of ground deformation.
Direction of deformation
InSAR measures in the direction along a straight line between a SAR antenna and the ground (the direction of the satellite's line of sight).
The SAR satellite transmits and receives a radio wave obliquely downward (obliquely upward from the ground). In addition, the track on which the satellite observes the ground from the East or the West is often used.
The ground movement is three dimensional (east and west, north and south, up and down) but InSAR can measure it in only single direction, in the LOS direction. So we cannot simply determine what direction the ground moved in.
The "LOS distance gets longer" means that the ground moved in the direction away from the satellite. In other words, if the satellite observes the ground from the East, the ground moved down or west. At this time, we cannot know whether the ground moved in the north-south direction. The ground might move down, west, or down-west. Otherwise the ground might totally move in the direction away from the satellite because the ground moved down-east but the downward component countered the east component. However we cannot find these difference.
The real amount of the ground movement is calculated from the geometrical relation between the incidence angle of the SAR radio wave transmitted to the ground and the direction of the ground movement. For example, if the ground movement results only from subsidence, the horizontal component of the movement is zero. So for ALOS off-nadir angle of 34.3 degrees, the amount of subsidence is about 1.3 times the amount of deformation in the LOS direction.
*Off-nadir angle:Angle between the vertical direction (nadir) from the satellite and the direction of the satellite' s line of sight.
 How to understand the SAR interferogram
How to understand the SAR interferogram